|
|
|||||
|
顺势加仓和逆势加仓详解(图解)
|
|||||
|
|
|||||
|
|
|||||
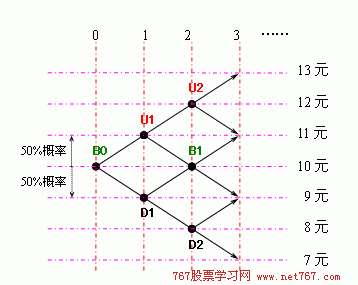
先来设想一个随机漫步的价格波动(看下面的图,大名鼎鼎的二叉树图):
1、期望收益为0的时候,加仓是没用的.
比方说:假设在B0处开多1手,
(1)顺势金字塔加仓 比如,如果价格下跌到D1则停损收手;如果上涨到U1,则加仓0.5手……那么可以计算这种顺势金字塔加仓的期望收益为:
可能性1:50%的概率下跌到D1,亏损1元,因为概率是50%,所以期望收益为50%×(-1)= -0.5; 可能性2:50%的概率上涨到U1,这时加仓0.5手,加仓后: 可能性2.1:50%的概率跌回B1,亏损0.5元,因为概率是(50%)2=25%,所以期望收益是25%×(-0.5)= -0.125; 可能性2.2:50%的概率涨到U2,总盈利2.5元,因为概率也是25%,所以期望收益25%×3= 0.625 所以,总的期望收益= -0.5-0.125+0.625=0,仍然是零。 (2)逆势金字塔加仓 比如,如果价格上涨到U1就止盈收手;如果下跌到D1,则加仓2手……那么: 可能性1:50%的概率上涨到U1,盈利1元,概率是50%,所以期望收益为50%×1= 0.5; 可能性2:50%的概率下跌到D1,这时加仓2手,加仓后: 可能性2.1:50%的概率涨回B1,盈利2元,概率是(50%)2=25%,所以期望收益为25%×2=0.5; 可能性2.2:50%的概率跌到D2,总亏损4元,因为概率也是25%,所以期望收益为25%×(-4)= -1 所以,总的期望收益= 0.5+0.5-1=0,还是零。 2、顺势加仓和逆势加仓的性质
同样以开多、等规模加仓为例: (1)顺势加仓 顺势加仓有一个很好的性质、也有一个很不好的性质。 1)好是好在它可以控制亏损的规模,同时放大盈利。 因为如果要实现加仓,那么第一仓一定是轻仓。比如,事先计划准备5次加仓,那么在等规模加仓下,就要把资金分成5份,在上面图中的B0处开多的资金只投入20%,这样,如果价格跌到D1的话,虽然跌幅是10%,但是总资金只亏损2%。 但是如果价格能一路涨到U3,那么在U1、U2两个地方将分别有等规模的加仓,累计将实现12%左右的总资金收益率。这样,一次的成功就可以顶上6次的失败。 2)不好的地方是顺势加仓会大幅度减少盈利交易的次数。
比如,按照上面的图中的假设,如果不采用加仓,则在B0处买多,平均每1000次中有500次是盈利的,价格会涨到U1。 但是,采用顺势加仓后,假设是等规模加仓,则在B0处买多1手之后,平均每1000次中有500次的价格会涨到U1,在U1处等规模加仓1手之后: 这500次中平均有250次会回到D2,虽然价格只是回到10元,但是由于在U1处加仓1手,所以总体上会亏损1元。 另外平均有250次会继续上涨到U2,按规则在U2处继续加仓1手。第二次加仓之后: 其中平均又有125次会跌到D3,这个时候虽然在B0处开的仓位是盈利1元,但是在U2处增加的仓位是亏损1元,所以总体上仅仅是打平; 另外平均有125次会继续上涨到U3,如果就次打住的话,总体上是可实现盈利6元。 这样,由于顺势加仓,亏损的交易次数的比例就增加到了75%,另外有12.5%的交易只能打平,只有12.5%的交易能实现盈利,虽然盈利会很大。 换一个角度,不加仓的时候,只要价格上涨就能实现盈利,但是顺势加仓之后,如这里所分析的,价格必须得至少连续上涨3段以上,才能实现盈利;连续上涨2段只能打平;如果只能上涨1段,那么最后的结果跟一开始就下跌是一样的。 也所以,可想而知,如果要采用顺势加仓的方法,必须对交易品种的上涨和下跌的空间有个事先的估计。最起码是应当是在估计空间能容纳3次以上的加仓的时候才能进场。 当然,因为采用等规模顺势加仓会使盈利次数下降得太厉害,所以有了正金字塔加仓,每次增加的仓位都比前一次的仓位小。到这里,已经能很容易理解,正金字塔加仓无非是一种折中,通过放弃一部分盈利时的盈利额,来提高盈利次数,以降低对心理的压力。
|
|||||
|
|||||
| 相关文章:
网格交易策略从基础到进阶(图解) |